.png)
If you haven't watched the video yet, here is the link :
if you don't speak Chinese, the question can be translated into the following :
"given that both 4 sided shapes are squares, find the area of the shade".
Teacher 柳 used the rotating method to rotate the Right triangle in order to calculate what is requested, but he is lucky that the triangle he is rotating is a right triangle, but what will happen if that triangle is not a right triangle?
And this took me a while to prove :
when you have 2 squares not overlapping, sharing the same vertex each with their corners, the two triangles adjacent to the 2 squares will have the same area.
and so here's the proof:
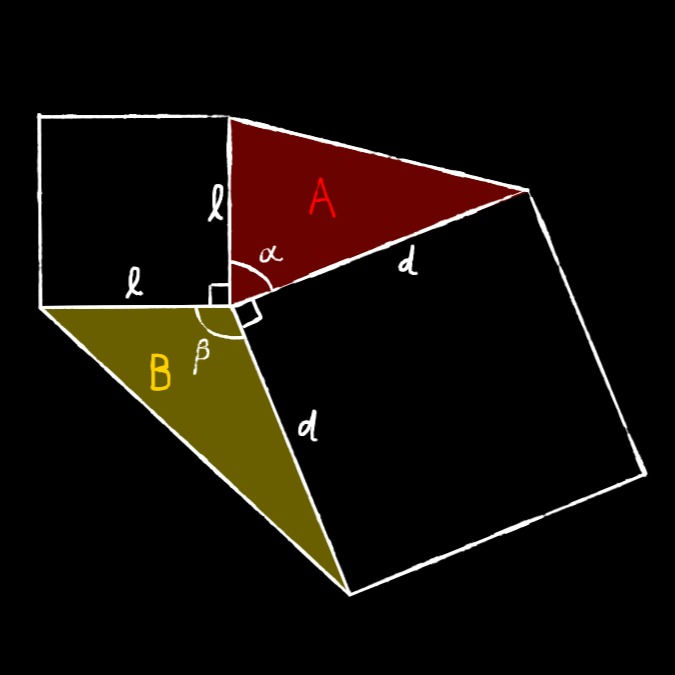
say the side of one of the squares is ℓ, and the other one is 𝑑,
let's call the 2 triangles A and B, with their angles α and β.
according to
∵ Area of a Triangle = 0.5 × a × b × sinθ
then we know that
A = 0.5 × ℓ × 𝑑 × sinα
B = 0.5 × ℓ × 𝑑 × sinβ
According to the diagram,
90° + α + 90° + β = 360°
α + β = 180°
∴ sinα = sin(180° - β) = sin180°cosβ - cos180°sinβ = 0 × cosβ - (-1)sinβ = sinβ
sinα = sinβ
0.5 × ℓ × 𝑑 × sinα = 0.5 × ℓ × 𝑑 × sinβ
A = B (Proof complete)
if the given situation is : w and 𝑑 and θ are given just like how the question given by him did
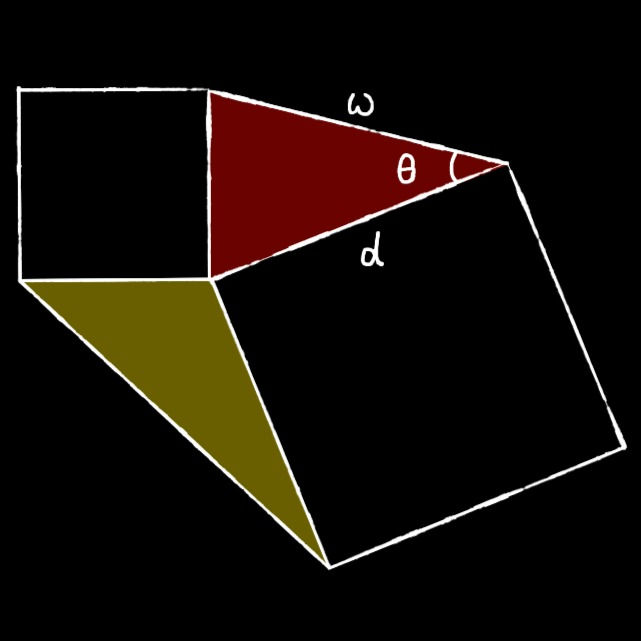
we can just simply use
A = 0.5 × w × 𝑑 × sinθ = B
Comments