.png)
Since we are upgrading our website, we have decided to compress all the Geometry proofs into one single post. Below are the contents of this post :
Angles:
The sum of the angles of any triangle is 180°
The sum of the inner angles of any polygon
Lines, Length & Distance:
Pythagoras Theorem
Sine, Cosine, Tangent specific value with specific angles
Areas:
Area of an obtuse triangle
Area of a trapezoid
The sum of the angles of any triangle is 180°
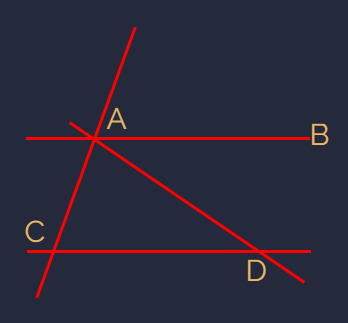
∵AB//CD
∴∠CAB + ∠ACD = 180°
∴∠CAD + ∠BAD + ∠ACD = 180°
∵AB//CD
∴ ∠BAD = ∠ADC
∴∠CAD + ∠ADC + ∠ACD = 180° (QED)
The sum of the inner angles of any polygon
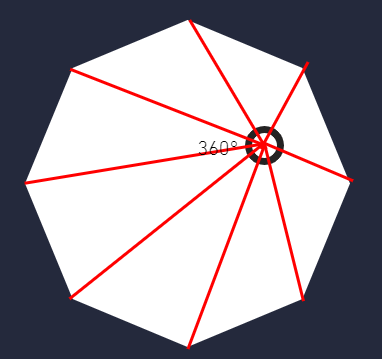
Let's suppose that we have a polygon with N sides, we can pick a point inside the polygon and start drawing lines from this point to all the vertices of the perimeter of the polygon,
∵ N-side polygons have N vertices
∴ we'll have N triangles.
∵ the sum of angles of a triangle is 180°,
∴ the sum of all the inner angles of the triangles is N x 180°
we have to remove the angles around the point we have chosen
(since the point we have chosen is not part of the polygon perimeter)
and the angle is 360° = 2 x 180°
so the sum of angles of a polygon is
N x 180° - 2 x 180° = (N-2) x 180°
Pythagoras Theorem
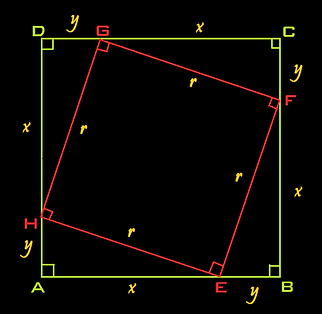
Here we have 2 squares: ABCD & EFGH,
which creates 4 right triangles with sides X, Y, R (the Hypothenuse).
Area of EFGH = Area of ABCD - 4 triangles
Area of EFGH = R²
Area of ABCD = (X + Y)²
Area of a triangle = ½ x XY
so
R^2 = (X + Y)² - 4 (½ x XY)
R^2 = X² + 2XY + Y² - 2XY
and finally
R² = X² + Y²
Sine, Cosine, Tangent specific value with specific angles
according to their graphs and definitions,
sine, cosine, and tangent are functions that express the scale of 2 sides of a right triangle but an acute angle must be chosen to determine which 2 sides will be selected for scaling.
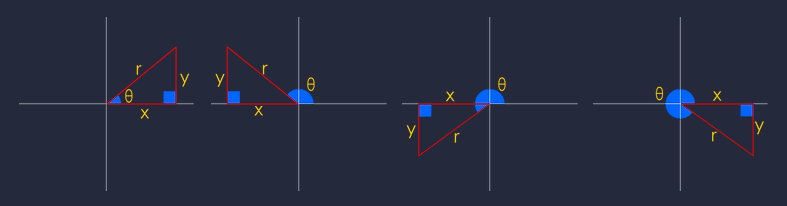
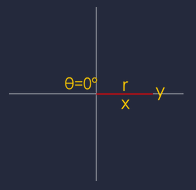
when θ=0°,
then x = 1,y = 0,r = 1
Function | definition | substitution |
sin | y/r | 0/1 = 0 |
cos | x/r | 1/1 = 1 |
tan | y/x | 0/1 = 0 |
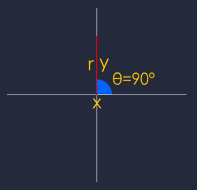
when θ=90°,
then x = 0,y = 1,r = 1
Function | definition | substitution |
sin | y/r | 1/1 = 1 |
cos | x/r | 0/1 = 0 |
tan | y/x | 1/0 = ERR |
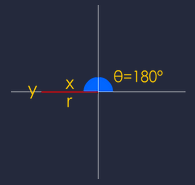
when θ=180°,
then x = -1,y = 0,r = 1
Function | definition | substitution |
sin | y/r | 0/1 = 0 |
cos | x/r | -1/1 = -1 |
tan | y/x | 0/-1 = 0 |
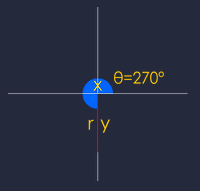
when θ=270°,
then x = 0,y = -1,r = 1
Function | definition | substitution |
sin | y/r | -1/1 = -1 |
cos | x/r | 0/1 = 0 |
tan | y/x | -1/0 = ERR |
and finally, here is a table to conclude what we have :
with similar approaches, we can get the values of other angles as well, in the table below, we are going to add in 30°, 45°, and 60° because these angles are very special angles that will form every specific vital triangle since things can be symmetrical here, we are going to only focus on the first Quadrant.
if a right triangle has a 30°, then that triangle has a chance to construct a hexagon, if a right triangle has a 45°, then it can be used to construct a square.
| 0° | 30° | 45° | 60° | 90° |
sin | 0 | 1/2 | 1/ √2 | √3 / 2 | 1 |
cos | 1 | √3 / 2 | 1/ √2 | 1/2 | 0 |
tan | 0 | 1/ √3 | 1 | √3 / 1 | #ERR# |
Area of an obtuse triangle
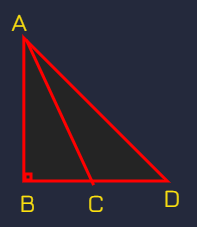
Let's say We want to find the area of the triangle ACD (an obtuse triangle)
area of ABD - area of ABC = area of ACD
area of ABD = AB x BD x ½
area of ABC = AB x BC x ½
area of ABD - area of ABC = (AB x BD x ½) - (AB x BC x ½)
= ½ x AB x (BD - BC)
= ½ x AB x CD
∴ Area of an Obtuse Triangle = ½ x height x "base"
Area of a trapezoid
AD⊥CE
AB // CE
Area of ΔABE = ½ x AB x AD
Area of ΔCAE = ½ x CE x AD
Area of ΔABE + Area of ΔCAE = Area of Trapezoid ABEC
½ x AB x AD + ½ x CE x AD
= ½ x AD x (AB + CE)
and finally
Area of a Trapezoid = ½ x Height x (Base1 + Base2)
And here we go, all 6 basic and important proofs.
Comments