Lightning Triangle
- XR_XharpRazor
- Aug 25, 2021
- 7 min read
M2007U-E2016-A2017-S2017-M2021_SMT-20200618x01

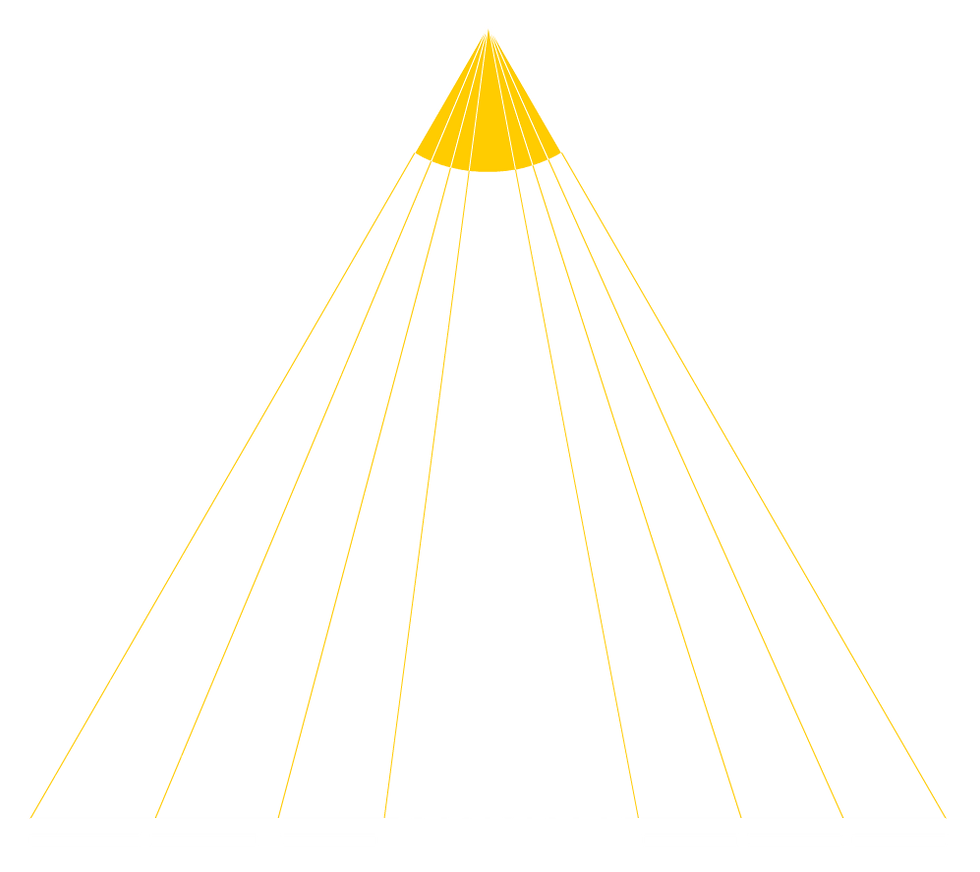
You must have played with some questions which asked you to count the quantity of some sort of object or shapes, took this diagram for example, how many triangles can you find from this diagram
Most of the people will just try to search all the triangles without any order, it is possible that they may overcount or miss some of the triangles.
"Thankfully, there is a way to count the triangles according to an order", yup, I said this when I shared this question to my classmates when I was 14 from my big family Whatsapp group, though this question is forwarded by my father.
Please note that this article is going to discuss ONLY the triangles which are similar to this type
Section 1
Let's look at the first part of the problem: a triangle (let's call this the General Yellow Triangle) with a bunch of lines connected from an angle to the base of the triangle
Let's define that a "Y Line"(or a "Yellow Line") is a line connected from the Angle (or let's call it "Y Angle") to the very base of the triangle.
Let's define that a "Base Segment" is a line segment
1) that is not connected to the Y angle
2) associated EXACTLY with 2 yellow lines (no other yellow lines touching it)
You can see each base segment is accompanied by a thin white rectangle.
3) a part of the base of the General Yellow Triangle
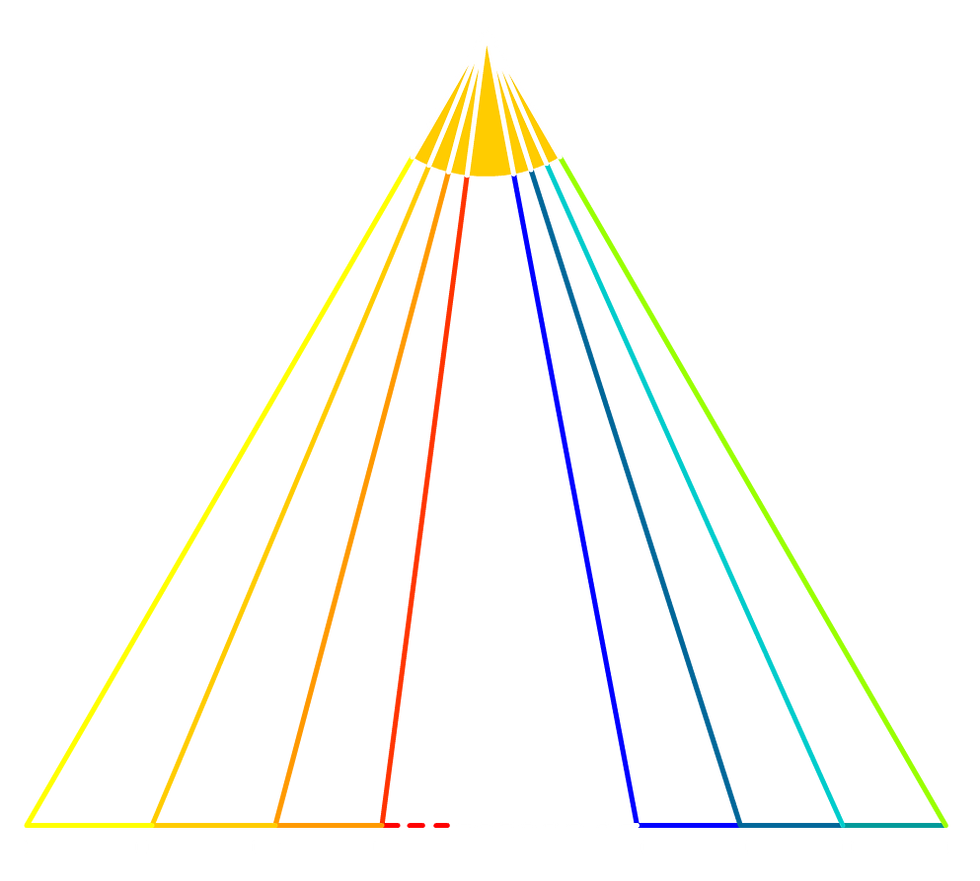
Let's match all the Y lines to a base segment by coloring it with the same color, notice that ONLY 1 Y line doesn't have a base segment.
Key point :
Numbers of Base Segment = Number of Y Lines - 1 = Y - 1 where "Y" is the Qty of Y Lines
A base of a constructed triangle in the General Yellow triangle can be a combination of Base Segments
Inside a base of a constructed triangle, Let's call the Base Segment on the left as "Base Head Segment" ( Orange Rectangle) , and the rest are "Base tail Segments" (White Rectangles)

Let's assign Y - 1 base Segments (all Base Segments we have so far) with Y - 1 brackets,
each Base Segment has its own brackets,
each Base Segments can be a Base Head Segment or a Base Tail Segment at the same time (except only the one on the left which only can be the Base Head Segment)
The bracket can be stretched ONLY to the right-hand side to cover multiple Base Segments.
Each bracket will construct a triangle with the width of Base Segments covered with the 2 Y lines connected with the base of the constructed triangle.
PS : Each White Rectangle is a Base Segment
Let's see how many triangles can be constructed with the brackets with a width of 1 Base Segment (1 Head 0 Tail)

The Yellow brackets should cover 1 Base Segment.
Notice that each bracket can construct a triangle with a base of 1 Base Segment.
let's jot that down as: Δ(1bS) = (Y - 1)
where "Δ(WbS)" means Qty of Triangles with a base of W Base Segments
where "Y" is the Qty of Yellow Lines, in this case, Y - 1 is the Qty of Base Segments
Now tet's see how many triangles can be constructed with the brackets with a width of 2 Base Segments (1 Head 1 Tail)

The Yellow brackets should cover 2 Base Segments.
Notice that each bracket can construct a triangle with a base of 2 Base Segment, except 1 colored red because it doesn't have a Base Segment as it's Base Tail Segment.
let's jot that down as: Δ(2bS) = (Y - 1) - 1
Now tet's see how many triangles can be constructed with the brackets with a width of 3 Base Segments (1 Head 2 Tails)

The Yellow brackets should cover 3 Base Segments.
Notice that each bracket can construct a triangle with a base of 3 Base Segments, except 2 colored red, because there are not enough base segments as their Base Tail Segments.
let's jot that down as: Δ(3bS) = (Y - 1) - 2
Now tet's see how many triangles can be constructed with the brackets with a width of 4 Base Segments (1 Head 3 Tails)

The Yellow brackets should cover 4 Base Segments.
Notice that each bracket can construct a triangle with a base of 4 Base Segments, except 3 colored red, because there are not enough base segments as their Base Tail Segments.
let's jot that down as: Δ(4bS) = (Y - 1) - 3
If we keep on going like this, we can get
Δ((Y-1)bS) = (Y - 1) - (Y - 2) = Y - 1 - Y + 2 = 1
If you look closer enough, you can know that:
Δ( W bS) = (Y - 1) - (W - 1) = Y - 1 - W + 1 = Y - W

If we collect all the notes we have, you can see the pattern
Δ( 1 bS) = (Y - 1) - (1 - 1) = Y - 1
Δ( 2 bS) = (Y - 1) - (2 - 1) = Y - 2
Δ( 3 bS) = (Y - 1) - (3 - 1) = Y - 3
Δ( 4 bS) = (Y - 1) - (4 - 1) = Y - 4
... and so on until
Δ( (Y-4) bS) = (Y - 1) - ((Y-4) - 1) = 4
Δ( (Y-3) bS) = (Y - 1) - ((Y-3) - 1) = 3
Δ( (Y-2) bS) = (Y - 1) - ((Y-2) - 1) = 2
Δ( (Y-1) bS) = (Y - 1) - ((Y-1) - 1) = 1
these are all the triangles that can be constructed from the General Yellow triangle. If we sum that up, we have
Δ(all with Y angle)
= 1 + 2 + 3 + 4 + ... + (Y-4) + (Y-3) + (Y-2) + (Y-1)
= (1 + (Y-1))(Y-1)/2
= (Y)(Y-1)/2
Section 2

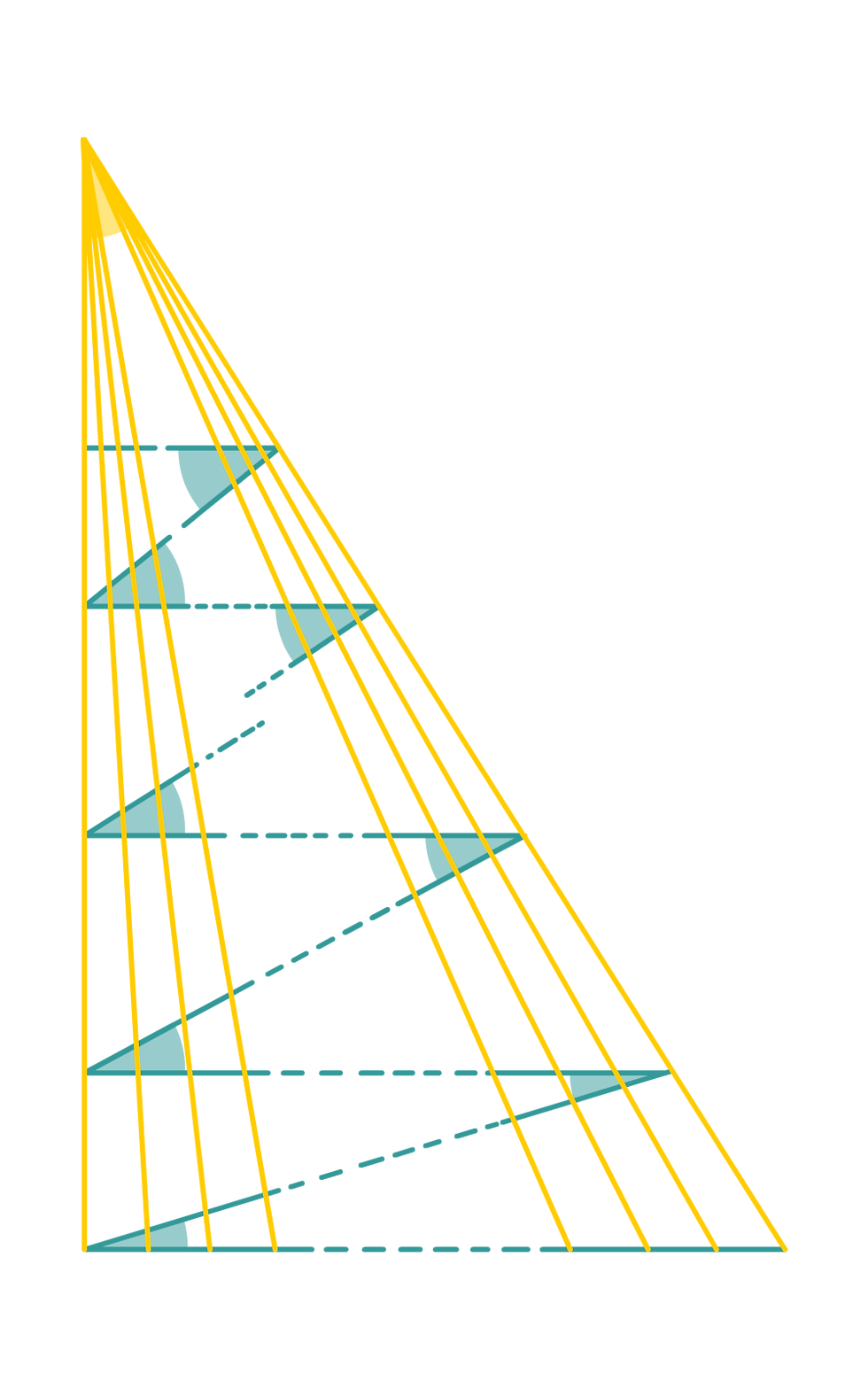
Let's look at the second part of the problem: a triangle (Let's call this the General Cyan Triangle) with a bunch of lines connected from side to side
Note that the lines connected from side to side will not intersect each other. And these lines are at the opposite of a shared angle, let's call this angle the C angle (Colored Cyan) and the Lines as "White Lines". There are 2 lines that are adjacent to the C angle (colored Cyan), so obviously enough let's call these 2 lines the Cyan Lines.
Let's define that a "Side Segment" is a line segment 1) that is connected to the C angle when extended or is within the Cyan Lines 2) associated EXACTLY with 2 White lines, except the one which is directly adjacent with the C angle, they only have 1 White Line Intersected You can see each side segment is accompanied by a thin white rectangle. 3) a part of the side of the triangle
The situation is much simpler than the first part of the problem.
If we try to match all the white lines to a Side Segment, Amazingly all of them are matched.
So we can get
Number of Side Segments = Number of White Lines
Let's assign each segment with a bracket, this bracket will construct a triangle with the angle C angle, notice that all triangles in this huge triangle will have to contain the C angle.
If we stretch all the brackets from their own "first" Side Segment to the "last" Side Segment, we can know that no brackets are red, meaning:
Number of Triangles it can make = Number of Side Segments = Number of White Lines
Section 3
Now. let's combine the General Yellow Triangle and the General Cyan Triangle together.
Noticed that
EACH CYAN LINE CAN CREATE A GENERAL YELLOW TRIANGLE WITH THE Y ANGLE ON THE TOP
AND
EACH YELLOW LINE CAN BE A WHITE LINE TO THOSE GENERAL CYAN TRIANGLES WITH THEIR C ANGLE COLORED
We know that in a General Yellow Triangle, there are
Y(Y-1)/2 triangles, then
X cyan Lines can make
XY(Y-1)/2 Triangles
Let's match each C angle to a Cyan Line, you will find that there is only 1 Cyan Line that is not matched, so that Line is unable to form a General Cyan Triangle
so we know that the
Number of General Cyan Triangles = X - 1
where X is the Qty of Cyan Lines.
Now just focus on a complete General Cyan Triangle, let's match each Yellow line to the White Lines, noticed that 1 of the Yellow lines is not a White Line available to the General Cyan Triangle, in fact, intersecting the C angles
So the Number of Available White Lines in these General Cyan Triangles = Y -1
since 1 General Cyan Triangle can make Y - 1 triangles,
then X-1 General Cyan Triangles can make
(X-1)(Y-1) Triangles
Finally, the sum of
XY(Y-1)/2 Triangles & (X-1)(Y-1) Triangles
is the total triangles it can make from this mess...
so the Formula would be
Qty of Triangle = XY(Y-1)/2 + (X-1)(Y-1)
where X is the Qty of Cyan Lines (Lines opposite to the Y angle), Y is the Qty of Yellow Lines(Lines connecting with the Y angle)
CAUTION: This formula this only applicable to ONLY these pattern-like triangles, especially the Cyan lines must connect in a zig-zag way, you have to extremely be careful to use it since small changes of the shape may alter the situation.
If the situation alters try to start with how many Y angles and C angles are there, and see if there are any new features.
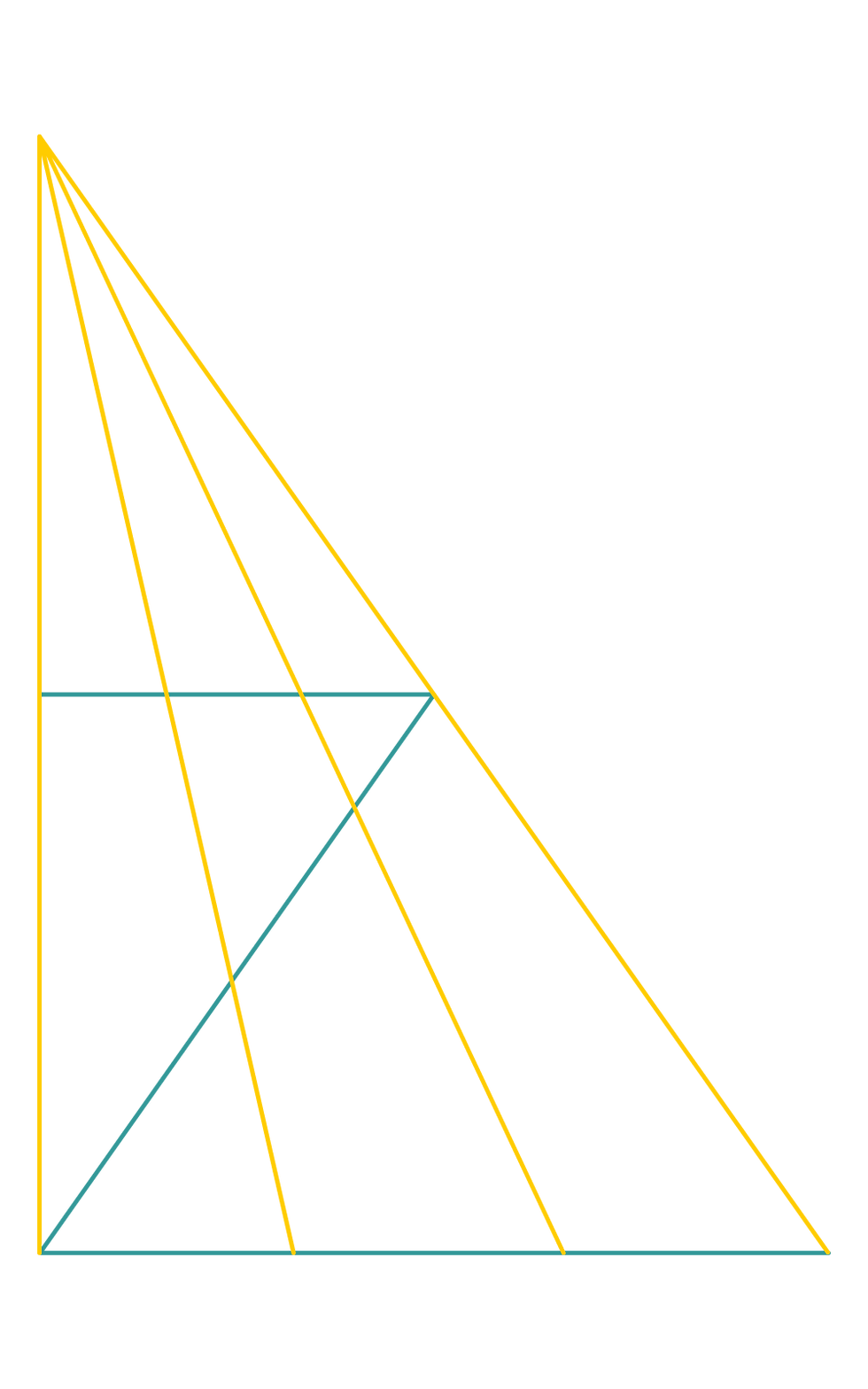
Now let's get back to the provided question we have,
as you can see we have 4 Yellow lines and 3 Cyan Lines,
So we know that X = 3, Y = 4, so plug that in, we get 24
And here's all of them
1st row : 1st General Yellow Triangle
2nd row : 2nd General Yellow Triangle
3rd row : 3rd General Yellow Triangle
4th row, 1~3 : 1st General Cyan Triangle
4th row, 4~6 : 2nd General Cyan Triangle


.png)



Comments