Sine Circle

M2007U-E2016-A2017-S2017-M2021_20180508x01

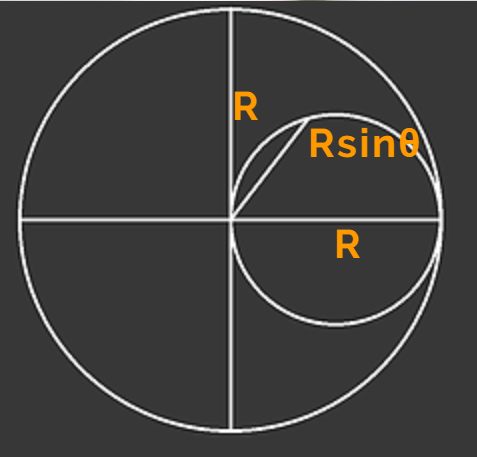
Let's draw a circle with a radius of R

and mark out all the angles with a factor of 5 degrees around the circle as the diagram shown on the right.

now let's mark out all different radii with a length of (R x the sine of the angle the radius is pointing to) from the center.

you'll find that the tips of those radii are likely to form a circle, the target of this article is to prove that the tips of the radius are really forming a circle.

Proofing

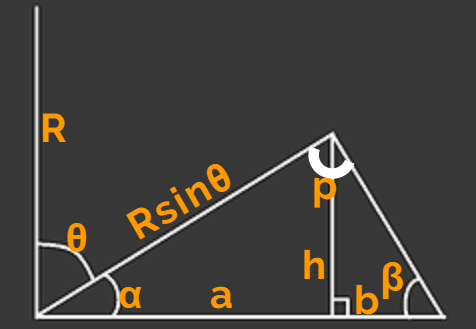
first, let's name the important parts of the setup:

R is the length of the radius of the big circle,

R = a + b

θ is the angle which the radius is pointing to,

Rsinθ is the length of the dynamic radii you've drawn

​the angle p is the one attached to the "likely circle"

to prove the "likely circle" is a circle, we just need to prove the angle p is a right angle.

first we need to define the range of θ, α, and β

in this case

0° ≤ θ ≤ 180°

0° ≤ α ≤ 90°

0° ≤ β ≤ 90°

from the diagram, we know that

∵ cosα = a / Rsinθ ..... equation (1)

∴ a = R ⋅ sinθ ⋅ cosα

∵ tanα = h / a ..... equation (2)

∴ h = a ⋅ tanα

∵ α + θ = 90° ..... equation (3)

∴ sinα = cosθ

∴ cosα = sinθ

starting with

tanβ = h/b

tanβ = (a ⋅ tanα) / b ..... from equation (2)

tanβ = (a ⋅ sinα) / (b ⋅ cosα)

sinβ / cosβ = (R ⋅ sinθ ⋅ cosα ⋅ sinα) / (b ⋅ cosα) ..... from equation (1)

cosβ / sinβ = (b ⋅ cosα) / (R ⋅ sinθ ⋅ cosα ⋅ sinα)

b = (cosβ)(R ⋅ sinθ ⋅ cosα ⋅ sinα) / (sinβ ⋅ cosα)

b = (cosβ/sinβ) ⋅ R ⋅ sinθ ⋅ sinα ..... equation (4)

from

R = a + b

R = R ⋅ sinθ ⋅ cosα + (cosβ/sinβ) ⋅ R ⋅ sinθ ⋅ sinα ..... from equation (1) and equation (4)

1 = sinθ ⋅ cosα + (cosβ/sinβ) ⋅ sinθ ⋅ sinα

1 = sinθ ⋅ sinθ + (cosβ ⋅ sinθ ⋅ sinα)/sinβ

1 = sin²θ + (cosβ ⋅ sinθ ⋅ sinα)/sinβ

1 - sin²θ = (cosβ ⋅ sinθ ⋅ sinα)/sinβ

cos²θ = (cosβ ⋅ sinθ ⋅ cosθ)/sinβ ..... equation (3)

cosθ = (cosβ ⋅ sinθ)/sinβ

cosθ / sinθ = cosβ / sinβ

tanθ = tanβ

θ = β

from

α + β + p = 180°

α + θ + p = 180°

90° + p = 180°

p = 90° ..... (proofed)

Usage

by measuring the length of Rsinθ and R and a simple calculator,

we can calculate the value of sinθ approximately：​

the length of Rsinθ / the length of R = the value of sinθ